插值

插值是一种通过已知离散数据点，在范围内求新数据点的方法，通过插值得到的近似函数一般是分段函数，所有的已知离散数据点都落在近似函数上
这种方式得到的函数可以用以已知数据范围内进行预测，在数据范围外可能会出现龙格现象，不建议进行预测

线性插值

线性插值是用一系列直线线段连接相邻的两个离散点，将这些直线作为近似函数

设n个离散点坐标为$ (x_i,y_i)$，那么在任意范围区间内，其高度应$y$由相邻的两个离散点所决定的线段确定

$y=y_i + \frac{x-x_i}{x_{i+1} -x_i} \times y_i$

假设我们有5个离散点

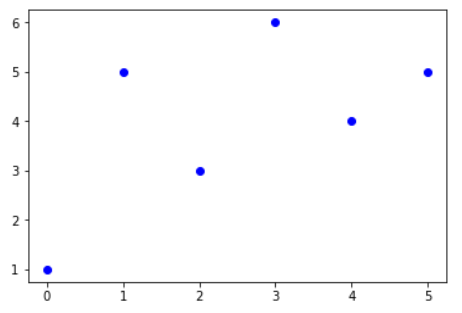
其插值后的图像应为

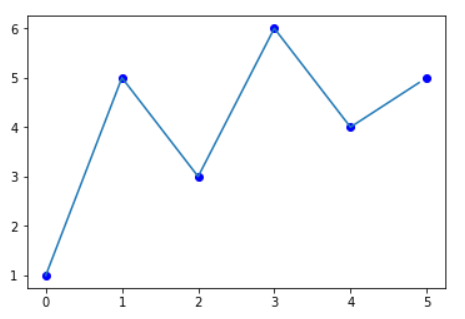
二次插值

既然线段能用来插值，那么我们很容易想到，那么曲线呢?
三个点能确定一条二次曲线，由此，我们用每三个点来确定一个区间的近似函数

$y = \frac{ (x-x_{i+1}) (x-x_{i+2})}{(x_i-x_{i+1})(x_i-x_{i+2})} \times y_i + \frac{ (x-x_{i}) (x-x_{i+2})}{(x_{i+1}-x_{i})(x_{i+1}-x_{i+2})} \times y_{i+1} + \frac{ (x-x_{i+1}) (x-x_{i})}{(x_{i+2}-x_{i+1})(x_{i+2}-x_{i})} \times y_{i+2}$

与线性插值进行对比

$y=y_i + \frac{x-x_i}{x_{i+1} -x_i} \times y_ = \frac{x-x_i}{x_{i+1}-x_i} \times y_{i+1} + \frac{x-x_{i+1}}{x_i - x_{i+1}}\times y_{i}$

可以看出形式都是一样的

lagrange插值

拉格朗日插值就是以上插值法的推广，用n个离散点确定一个范围区间内的近似函数

$y = \sum{l_i \times y_i}$ $l_i = \prod{\frac{x-x_k}{x_i-x_k}}$

样条插值

虽然上述插值法在各个区间内光滑，但可以预想，在区间与区间的分界点会有一个很差的光滑性
为了克服这个问题我们需要让分界点处光滑，即左右导数相等

样条插值采用待定系数法

假设有m+1个离散点， $(0,1…..m)$
进行n次样条插值(即每个点都在一条n次曲线上)
除去第m个点，对于每个离散点都可列出 $S_i(x), x \in [x_i,x_{i+1}]$ 如三次样条插值 $S_i(x)=a_i \cdot (x-x_i)^3 +b_i\cdot (x-x_i)^2+c_i\cdot(x-x_i)+d_i$ m+1个离散点我们应列出m个式子，即引进(n+1)m个未知数，需要(n+1)m个等式才能确定这些未知数
点在函数上 $S_i(x_i) = y_i$， m+1个等式
函数连续 $Si(x_i) = S{i+1}(x_i)$，排除掉左右端点有m-1个等式
导数连续 $Si^{(k)}(x_i)=S{i+1}^{(k)}(x_i)$，可求n-1阶导，排除掉左右端点有(n-1)(m-1)个等式
上述总计(n+1)m-(n-1)个等式，而最后的n-1个等式根据选择的不同插值法而确定
如三次样条插值，可设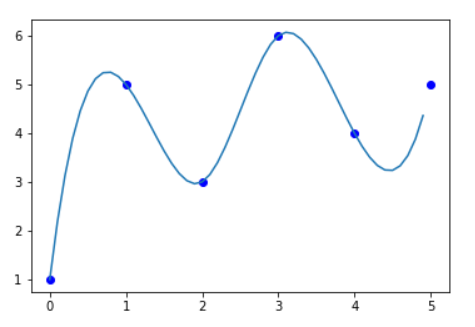 $S^{(2)}(x_0) = S^{(2)}(x_m) = 0$

拟合

拟合是把离散点用一条光滑曲线连接，与插值最大的不同在于其并不强制要求离散点一定在近似函数上
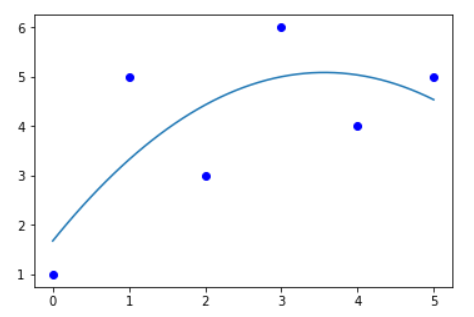
对于任意的数据，我们期望拟合一条$f(x)$使得各个离散点总体来看尽可能地贴近这条函数曲线
这种方式得到的函数可用来在已知数据范围附近进行预测

可设

$loss = \sum(f(x_i)-y_i)$

我们的目的是尽可能缩小$loss$
通过求$grad(loss)$，逐步更改未知参数，即可缩小$loss$

二次函数拟合图像