多元统计分析

多元统计分析是一种应用降维思想，去寻找变量之间关系并给出评价的方法
~~上课没认真听讲，这部分不太懂~~
参考的教程

假设我们有如下数据

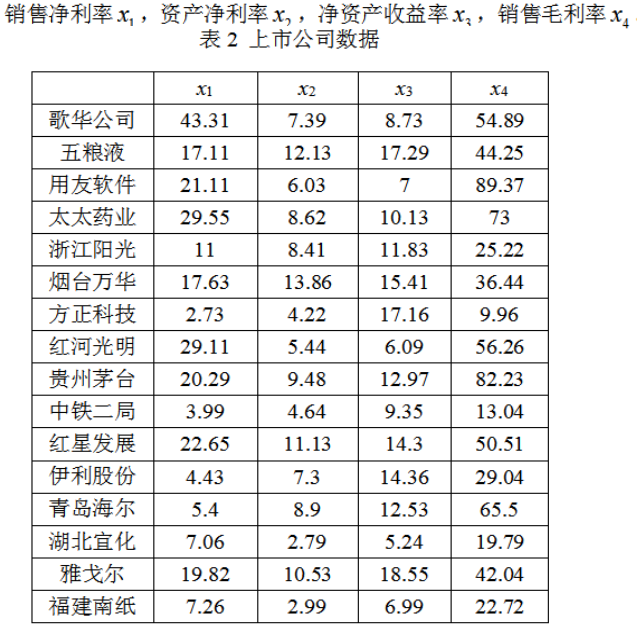
如何对所有公司进行综合评价并排序呢？

X为n维观测变量，如上为4，其均值为$\mu$，协方差矩阵为$\sum$
假定X可以表示为m个公共因子和n个特殊因子的线性组合 $\begin{bmatrix} X_1\\ X_2\\ \vdots\\ X_n \end{bmatrix} - \begin{bmatrix} \mu_1\\ \mu_2\\ \vdots\\ \mu_n \end{bmatrix} = \begin{bmatrix} l_{11} & l_{12} &\cdots & l_{1m} \\ l_{21} & l_{22} &\cdots & l_{2m} \\ \vdots & \vdots &\ddots & \vdots \\ l_{n1} & l_{n2} &\cdots & l_{nm} \end{bmatrix} \begin{bmatrix} F_1\\ F_2\\ \vdots\\ F_m \end{bmatrix}+ \begin{bmatrix} \varepsilon_1\\ \varepsilon_2\\ \vdots\\ \varepsilon_n \end{bmatrix}$ 即 $X_{n\times1} = \mu + L_{n\times m}F_{m\times1}+\varepsilon$

继续假设

$E(F)=0, Var(F)=E(FF^T)=I_m (不太理解$
$E(\varepsilon)=0, Var(\varepsilon) = E(\varepsilon\varepsilon^T)=\Psi=diag{\psi_1,\psi_2,\cdots,\psi_n}$
$cov(F,\varepsilon)=0$

在该假设下有(不清楚怎么推的)

主成分分析

运用参数估计的想法，估计$\sum$和$\Psi$

$\hat{L} =(\sqrt{\hat{\lambda_1}}\hat{e_1},\cdots,\sqrt{\hat{\lambda_m}}\hat{e_m})$
$\hat{\Psi}=diag(\hat{\psi1},\cdots,\hat{\psi_n}), \hat{\psi_i}=s{ii}-\sum{j=1}^{m}\hat{l{ij}}$
其中$S$是样本协方差矩阵，$\lambda$是特征值，由大到小，$e$是对应的特征向量

~~反正我也没搞懂，总之~~