0%

舞蹈链及数独解法

发表于

舞蹈链—精确覆盖问题

在正式介绍舞蹈链之前，先让我们明白其应用的问题—精确覆盖问题

精确覆盖问题

该问题是关于判断一个集合是否是一个精确覆盖的问题

满足以下条件的集合为一个精确覆盖：

  • S是全集X的部分子集的集合
  • S中任意两个集合没有交集
  • S中所有集合的并集为全集X

举例

X={1,2,3,4}O={1,3},E={2,4},U={1,2,3},D={1,3,4}

那么

{O,E}就是X的一个精确覆盖

若1,2,3,4分别代表一类约束条件，那么求满足条件的解，就是求X的精确覆盖

用01矩阵表示子集与全集的关系

  • 列是全集元素，
  • 行是子集
  • Aij=0代表子集i中不存在j元素

上述例子用01矩阵表示

[1010010111101011]

我们可以看到，精确覆盖在矩阵中表现出一种特点

  • 每一列在被选中的行(子集)中，有且仅有一个1

交叉十字循环双向链

在舞蹈链算法中，我们使用交叉十字循环双向链存储矩阵
这有几点好处

  • 由于01矩阵很可能是稀疏矩阵，所以只为值为1的位置创建节点能节省空间
  • 假如我们有A、B、C三个连续节点，删除B只需进行操作
    B.left.right=C，B.right.left=A
    而在回溯恢复B时，只需进行操作
    B.left.right=B,B.right.left=B

舞蹈链求解

把上述例子用交叉十字循环双向链表示

例1

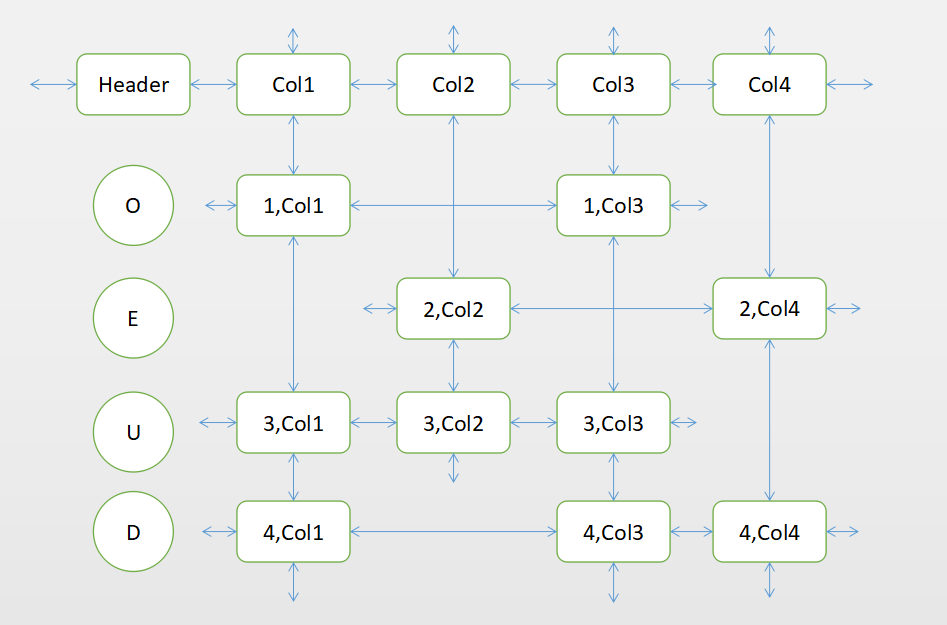
  • 方形节点是我们实际中要创建的节点，包括头结点、列首节点与所有的1节点
  • 所有1节点中将额外保存其行标和列首节点的指针
  • 找到解的条件是头结点的左右节点是他自己(这代表着所有列元素都被覆盖，会在接下来的步骤继续解释)

步骤一

  1. 取得Header右节点，Col1且Col1有其余节点
  2. 为了覆盖Col1，那么行1、3、4中一定有一个是解的一部分，把行1先放入答案
  3. 行1覆盖了列1、列3，为了不重复覆盖，我们先删除同样覆盖列1、列3的行

得到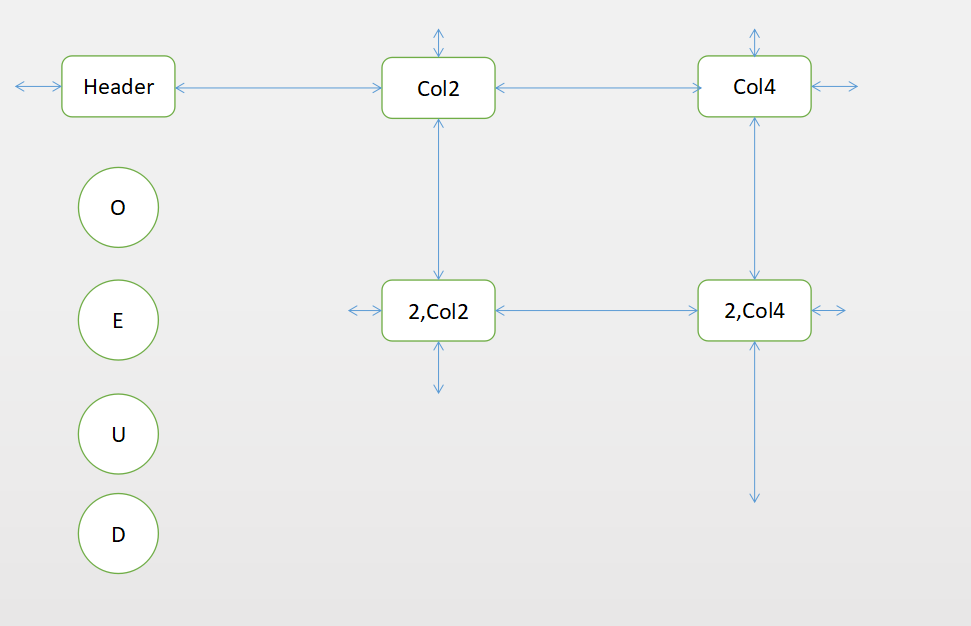
例2

步骤二

重复上述步骤，将行2放入答案

得到

3

步骤三

由于Header的左右节点是其自己表示已找到解

If

这看起来很顺利，那如果第一次选择的答案是行3，会是如何呢

  1. 行3覆盖了列1、列2、列3
  2. 删除对应行与列

得到

4
这时，我们发现Header右节点Col4下没有其余节点，这表示查找失败，准备回溯

代码细节

代码基于Python3

  • 在删除时，会将列首节点与左右断开，同时将非本列的节点与上下断开 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    def RemoveCol(self, c):
        '''
        删除列首节点及对应行
        :param c: 列首节点
        '''
        c.right.left = c.left
        c.left.right = c.right
        i = c.down
        while i!=c:
            j = i.right
            while j!=i:
                j.down.up = j.up
                j.up.down = j.down
                j.col.size-=1
                j = j.right

            i=i.down
  • 恢复节点是与删除完全相同的逆操作
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    def ResumeCol(self, c):
        '''
        恢复列首节点及对应行
        :param c: 列首节点
        '''
        i = c.up
        while i != c:
            j = i.left
            while j != i:
                j.up.down = j
                j.down.up = j
                j.col.size+=1
                j = j.left
            i = i.up
        c.right.left = c
        c.left.right = c
  • 主要递归函数，每次获取元素最少的列有利于加快速度，每次递归中，被删除的列的顺序与被恢复的列的顺序也是相逆的
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    def Solve(self):
        '''
        递归解决问题
        '''
        if self.Header.right == self.Header:
            for i in self.ans:
                self.matrix[i[0]][i[1]] = chr(ord('0')+i[2])
            return True

        c = self.get_min_size_col()
        self.RemoveCol(c)

        i = c.down
        while i!=c:
            self.ans.append(i.grid)

            j = i.right
            while j!=i:
                self.RemoveCol(j.col)
                j = j.right

            if self.Solve():
                return True
            self.ans.pop(-1)

            j = i.left
            while j!=i:
                j = j.left

            i = i.down
        self.ResumeCol(c)

        return False